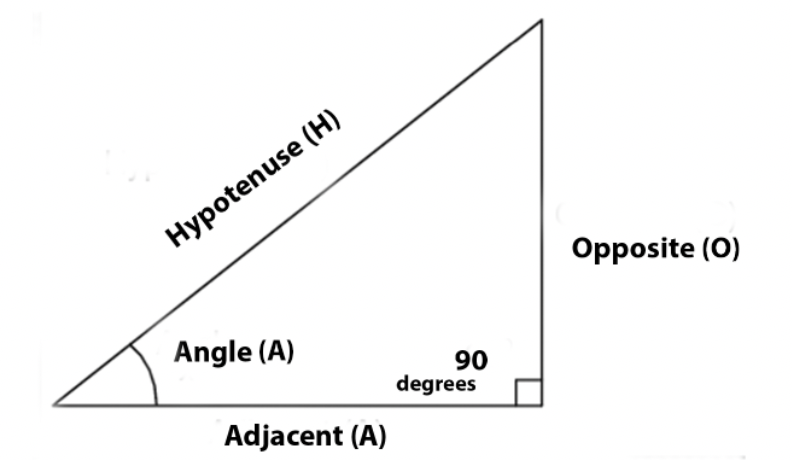
An adjacent side in a triangle is a side that is next to or shares a vertex with another side. Adjacent sides in a triangle are important for understanding the relationships between the sides and angles of a triangle.
Definitions:
- Triangle: A polygon with three sides and three angles.
- Side: A line segment that is part of the boundary of a polygon.
- Vertex: The point at which two or more lines or line segments meet.
There are three sides in a triangle and three angles. The sides of a triangle are typically referred to as side A, side B, and side C. The angles of a triangle are typically referred to as angle A, angle B, and angle C.
In a triangle, there are three pairs of adjacent sides. Side A is adjacent to side B and side C. Side B is adjacent to side A and side C. Side C is adjacent to side A and side B.
The adjacent sides of a triangle are important for understanding the relationships between the sides and angles of a triangle. For example, the adjacent sides of a right triangle (a triangle with one right angle) are the sides that form the right angle. The adjacent sides of an isosceles triangle (a triangle with two equal sides) are the two equal sides.
Examples:
Example 1:
Consider a triangle with sides of length 5, 12, and 13. Side A is adjacent to side B and side C. Side B is adjacent to side A and side C. Side C is adjacent to side A and side B.
Example 2:
Consider a right triangle with sides of length 3, 4, and 5. Side A is the hypotenuse (the side opposite the right angle) and is adjacent to side B and side C. Side B is adjacent to side A and is one of the legs of the right triangle. Side C is adjacent to side A and is the other leg of the right triangle.
Example 3:
Consider an isosceles triangle with sides of length 6, 6, and 8. Side A is adjacent to side B and side C. Side B is adjacent to side A and is one of the equal sides. Side C is adjacent to side A and is the other equal side.
Example 4:
Consider an equilateral triangle with sides of length 6. All three sides are equal in length and are adjacent to each other.
Example 5:
Consider a scalene triangle (a triangle with no equal sides) with sides of length 3, 4, and 5. Side A is adjacent to side B and side C. Side B is adjacent to side A and side C. Side C is adjacent to side A and side B.
Quiz:
- Which of the following is not a side of a triangle?
a) Side A b) Side B c) Side C d) Side D
Answer: d) Side D
- Which of the following is not an angle of a triangle?
a) Angle A b) Angle B c) Angle C d) Angle D
Answer: d) Angle D
- Which of the following triangles is a right triangle?
a) A triangle with sides of length 3, 4, and 5 b) A triangle with sides of length 5, 12, and 13 c) A triangle with sides of length 6, 6, and 8 d) A triangle with sides of length 6
Answer: a) A triangle with sides of length 3, 4, and 5









